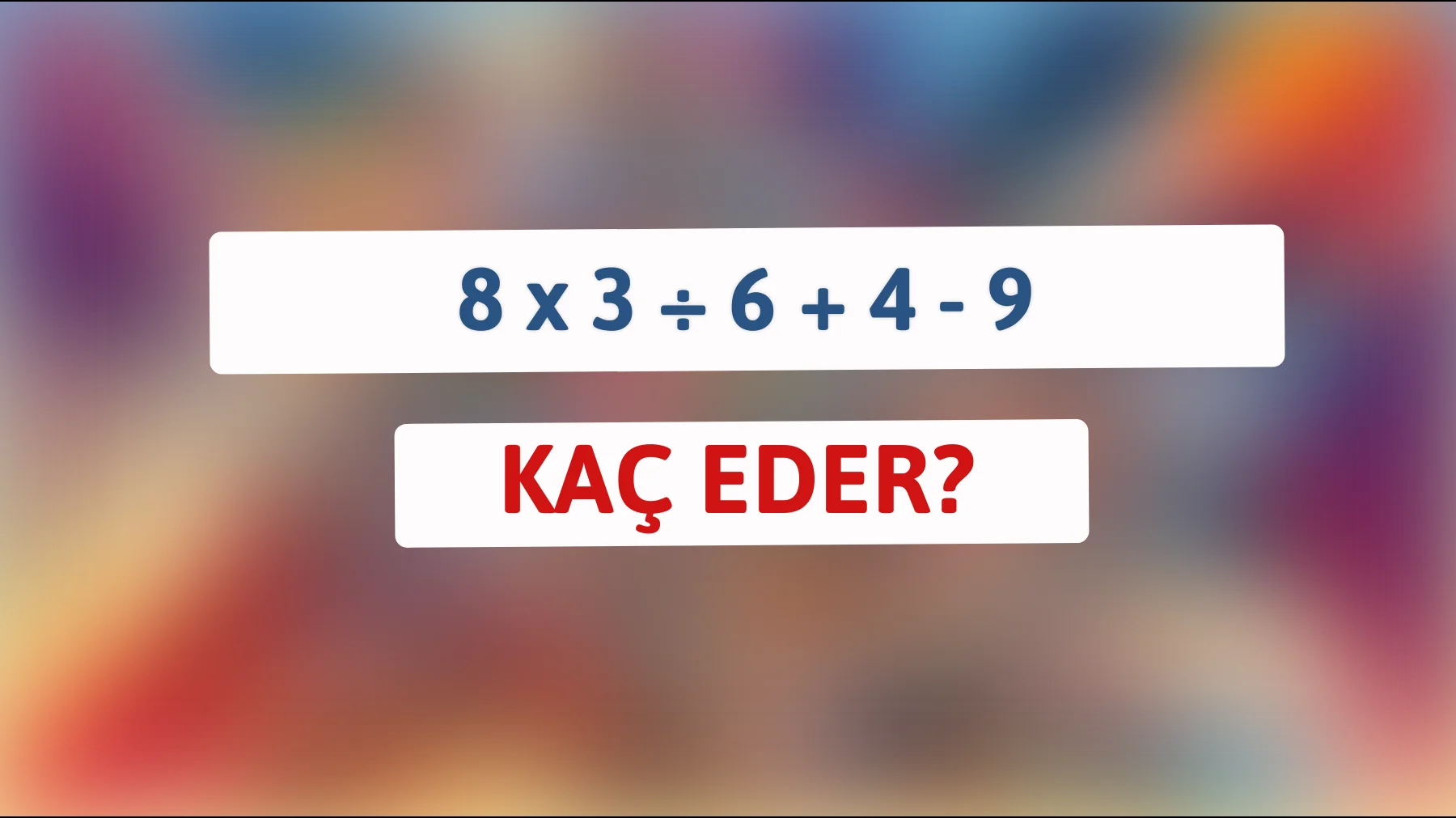Matematiksel bilmece sever misiniz? İşte beyninizi zorlayacak bir işlem: Kaç eder 8 x 3 ÷ 6 + 4 – 9? Cevabı hemen bulup bulamayacağınızı merak ediyoruz! Hem eğlenecek hem de zihninizi çalıştıracaksınız.
Genellikle basit görünen aritmetik işlemler, küçük bir hata, dikkatsizlik veya aceleyle büyük karışıklıklara yol açabilir. Özellikle, operasyonların sırasını göz ardı edersek işler daha da kafa karıştırıcı hale gelebilir. Matematik, yalnızca bir sonuç bulmaktan daha fazlasıdır; mantık ve yöntemle ilgili bir oyundur. Şimdi, bir an için durup bu basit gibi görünen işlemin derinliklerine inelim.
İlk bakışta, “8 x 3 ÷ 6 + 4 – 9” işlemi oldukça basit gözükebilir. Ancak her bir operatörün nasıl ve ne zaman kullanıldığı, doğru sonuca ulaşmak için önemlidir. Matematikte genellikle takip ettiğimiz bir temel kural dizisi vardır: İşlemlerin sırası. Parantez, üslü ifadeler, çarpma ve bölme ile toplama ve çıkartma… Bunlar, doğru sonuca ulaşmak için takip etmemiz gereken adımların birer parçasıdır.
Matematik Bilinmeyenlerini Çözerken Dikkat Edilmesi Gerekenler
İşlemi adım adım çözmek, sonuçların doğruluğunu sağlamak açısından kritiktir. İlkin çarpma ve bölme işlemlerine odaklanmamız gerekir. Burada, **8 x 3 = 24** olarak ilk adımımızı attık. Yani çarpma işlemi. Sonrasında, bu sonucu **24 ÷ 6** ile **4** olarak bulmayı başardık. İlk iki adımı başarıyla tamamladınız. Şimdi ise bu sonucu toplama ve çıkarma işlemleriyle birleştirme zamanı.
Devamında, elimizdeki **4** sonucuna, işlem sırası gereği **+ 4** ekliyoruz ve elde edilen sonuç **8** oluyor. Şimdiye kadar köprüyü yarıladınız, ama önemli olan bitiş çizgisine en doğru şekilde ulaşabilmek! İşlemin son basamağında, bu toplamdan **- 9** çıkardığımızda, nihayet aradığımız sonuca ulaşıyoruz: **-1**.
Negatif Sayıların Sihri: -1
Nihayetinde ulaştığımız sonuç -1, pek çok kişi için basit bir sayı gibi gelebilir. Ancak matematikte -1, oldukça ilginçtir. Negatif bir sayı olmasının ötesinde, matematikte daha derin bir dünya olan karmaşık sayıların kapısını aralar. Negatif sayılar, özellikle de -1, bir sayının işaretini değiştirmesiyle bilinir. Bu işlevsellik, matematiksel işlemlerde birçok önemli role sahiptir. Örneğin, kartezyen düzlemde eksenlerin zıt yönlerini işaret eder. Bu anlamda -1, matematikçinin elinde çok yönlü bir araçtır.
Bu yazıda, basit bir matematik işlemi üzerinden, mantık yürütmenin ve dikkatli adım atmanın önemi üzerinde durduk. Unutmayın ki, her sayı ve her işlem, düşündüğünüzden daha fazla anlam taşıyor olabilir. Matematik, yalnızca sayılarla değil, kafanızın içindeki bulmaca kutusuyla oynamanızı sağlar. Şüphesiz ki, bir sonraki matematiksel sorun için hazırlıklı olmak isteyeceksiniz!